3 Ways To Make Degree Symbol in Windows MS Word – Making the degree Celsius symbol is probably very easy for us to do on a sheet of plain paper, but what if we want to insert the symbol or sign in a data processing program such as Microsoft Word.
Table of Contents
How to Make Degree Symbol in Windows MS Word 2023
So, in this article, we will review how to write a degree symbol in Word very easily and quickly, of course.
Read more:
- How to Install and Use Apple Notes on Windows 10
- How to Activate Microsoft Office 2019 Permanently Offline
- How to Install And Activate Corel Draw X7 on Windows
- How To Activate Windows 7 Permanently Offline
When we try to enter the degree symbol in Ms Word, we have a little trouble, this is because the computer or laptop keyboard is not available.
Some of them are the Rupe symbol, th, 1st, phi, tick, or checklist, and other symbols that are still related to writing a physics or mathematical formula.
No need to wait too long, let’s just discuss the easy technique guide for typing the degree symbol in Word.
How to make a degree symbol in Microsoft Word Windows 10
The tips for making this degree symbol apply to all versions of Microsoft Word starting from 2007, 2010, 2013, and 2016.
Well, Windows Phone users can adjust it themselves. Because basically, it is not much different when using a computer or PC.
#1. Superscript
This first method is highly recommended to try, how to quickly create a degree symbol in Word is very easy and practical because it only uses a combination of keyboard keys.
Steps to create a degree symbol in Word
1. Open a Microsoft Word data processing program on your computer or laptop.
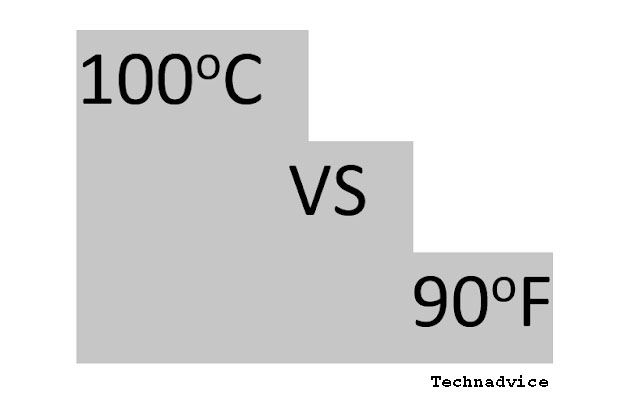
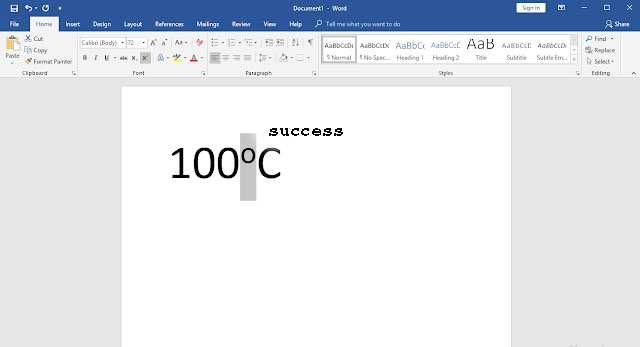
2. After that you type freely, here I write the number 100 degrees Celsius as an example.
3. Well, as for the writing use the following format.
- 100oC
- 100 is a number
- o is the lowercase o
- C is the capital C
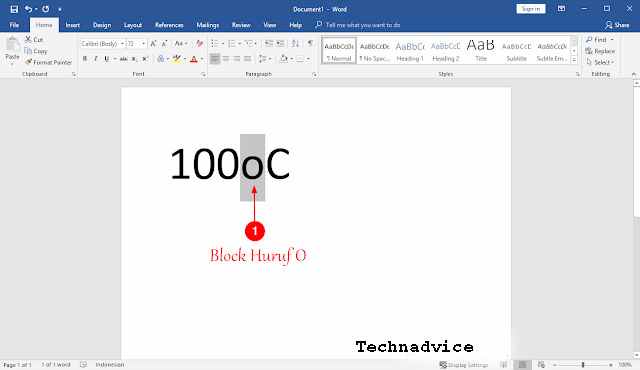
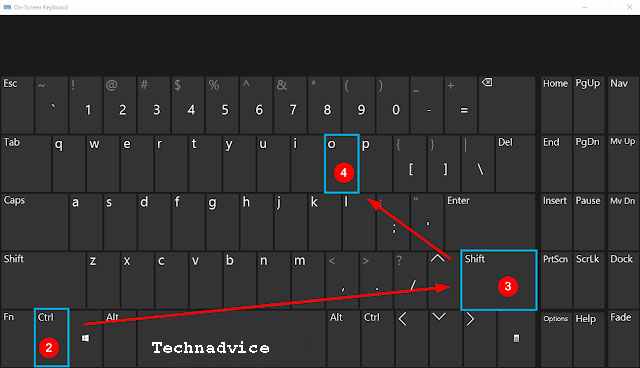
4. If you have selected or blocked the lowercase o by using the cursor or Shift + Right or left direction.
5. Finally, you can press the key combination Ctrl + Shift + O. Then automatically the lowercase o will go upwards to become a degree symbol.
You can also use this Superscript feature by going to the Home menu tab and then selecting the last font you click the X rank.
#2. Symbol
In this second alternative, we will take advantage of the menu facilities found in MS Word. Not only the degree symbol, but you can also make Arabic writing in Microsoft Word.
Steps to writing degree symbol in MS Word
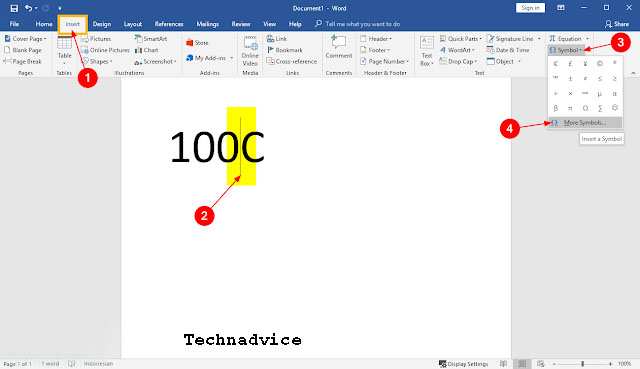
1. Please open the Insert Menu tab as shown below.
Then you type the number 100C, right before the letter C You place the cursor in front of it.
2. Enter the Symbol function in the upper right corner, and press it to open the dropdown menu. Click on the very bottom itself, More Symbols, to get a choice of various symbols or other special characters.
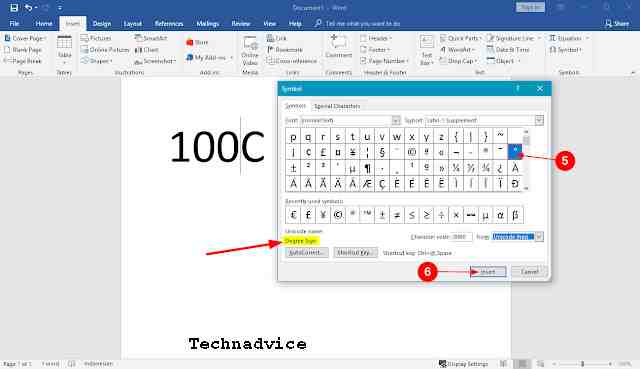
3. After that the usual Symbol pop-up menu will appear, you open it in the Symbols section, and you select the character.
Well, to make sure that it’s a degree symbol or not. You can see it in the Unicode name: Make sure it is labeled Degree Sign.
4. Finally, you can press the Insert button to enter it. If it is successful you can select the Close button to close it.
#3. Equation
Maybe for those of you who often enter mathematical formulas such as making orders or others, you must be familiar with the Equation feature.
Well, it turns out that in this function we can make a degree symbol too. Here’s the guide.
Steps to enter the degree symbol in Microsoft Word
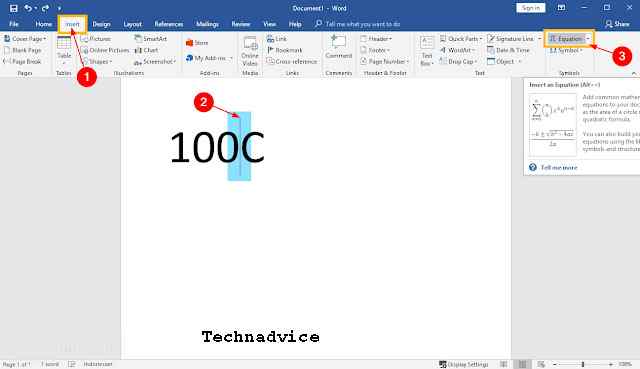
1. Please open the Insert Menu tab on the MS Word sheet.
2. Then you write something like this 100C. If you have now, place the cursor right in front of the letter C as shown.
3. You enter the Equation feature to select the symbol or formula to be used.
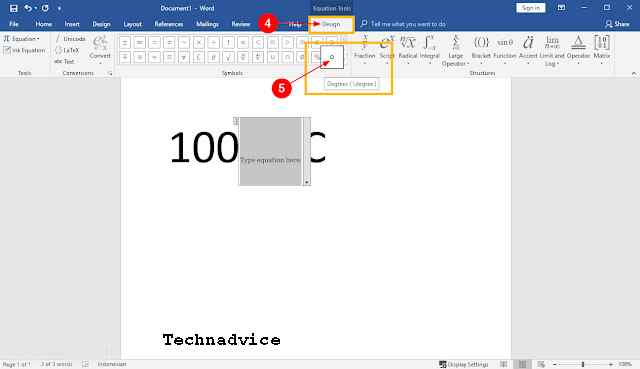
4. Enter the Design menu tab and select the degree symbol usually labeled Degrees (\ degree). Then the degree symbol will automatically be inserted right before the letter C.
By using the Equation feature you can also insert other symbols such as percent (%), multiplication, division, and so on.
If you look at some of the methods that we have discussed above, you can not only insert the degree Celsius (ºC) symbol. It can also create a degree Fahrenheit (ºF) symbol. Until the exponent or square root can also be.
Well, additional tips if you use them in large enough quantities. You can use the copy-and-paste function.
Read more:
- How to Activate Microsoft Office 2010 Permanently Offline
- How To Error Windows Explorer Has Stopped Working
- How to Fix Windows Script Host Disabled 5 Best Ways
Conclusion:
So, friends, This is the explanation of how to make a degree symbol in windows MS word, use this symbol is often applied to data processing programs such as Microsoft Word, Excel, and PowerPoint.
Hopefully, this tutorial on how to make a degree symbol in Microsoft Word will help you. Now it’s not easy to write Celsius or Fahrenheit symbols on your worksheets.
Don’t forget to bookmark and always visit every day Technadvice.com because here you can find the latest technology information such as How-to Guide Tips and Tricks Blogging Digital Marketing Windows Android Root Social Media games, ETC. Best of luck.
